21.12.2013, Götz-Anders Nietsch. (Dieser Beitrag erschien bereits in Heft 5/2013 der SVAOe-Nachrichten. Er könnte aber auch eine weitere Leserschaft interessieren und wird hier mit geringfügigen Ergänzungen wiedergegeben)
Wie selbstverständlich legen wir das Dreieck auf die Seekarte und ziehen mit dem Bleistift eine gerade Linie von A nach B: Das ist der Kurs, den wir segeln wollen, der „Kartenkurs“, wie er nach DIN 13312 korrekt heißt. Der Winkel, den die Kurslinie mit dem auf der Karte nächstgelegenen Meridian bildet, und den wir durch Parallelverschieben des Kursdreiecks ablesen, ist unser Kurswinkel, den wir nach entsprechender Beschickung am Kompass steuern. Auch wenn wir das Kursdreieck nicht zum nächstgelegenen Meridian, sondern zu einem beliebigen anderen, viel weiter entfernten, verschoben hätten, wäre dasselbe Ergebnis herausgekommen.
Was erzähle ich hier überhaupt diese Trivialität? Jeder weiß doch, dass das der Merkatorprojektion der Seekarten zu verdanken ist, bei der alle Meridiane parallel verlaufen. Moderne Menschen brauchen vielleicht keine Papierseekarte und kein Kursdreieck mehr, aber sie machen mit elektronischen Hilfsmitteln dasselbe. Wer navigiert, braucht eine geometrisch einfache Methode und einen zumindest abschnittsweise gleichbleibenden Kurs, um auf der gekrümmten Erd- und Meeresoberfläche ans Ziel zu kommen und möchte alles anschaulich auf einer ebenflächigen Darstellung sehen können.
Ich komme auf diese allseits bekannten Dinge zu sprechen, weil einerseits Mercators Geburt die bemerkenswerte, runde Zahl von 500 Jahren zurück liegt und andererseits immer wieder festzustellen ist, dass seine bis auf den heutigen Tag bahnbrechende Erkenntnis nicht richtig verstanden oder falsch dargestellt wird. Das hat er nicht verdient. Allerdings hat er auch ein bisschen selbst dazu beigetragen.
Die „Yacht“ widmete dem Jubiläum immerhin in Heft 17/2012 einen Beitrag, doch schon mit dem Untertitel „Mercators Methode war so einfach wie genial“ lag sie ziemlich daneben. Denn einfach war sie nicht, wie ein nicht Mathematik-affiner Leser im folgenden feststellen wird. Die „Yacht“ verstieß gegen Einsteins berühmten Satz „Erkläre die Dinge so einfach wie möglich, aber nicht einfacher“ und simplifizierte über das zulässige Maß hinaus, bis es falsch wurde. Aber die „Yacht“ steht da nicht alleine. Jeder sucht gerne einfache Erklärungen, aber sie sind nicht immer richtig.
Gehen wir also an die Quellen zurück, mitten ins sechzehnte Jahrhundert. Das war nicht nur das Ende der Renaissance, dieser kreative Ausbruch aus dem Mittelalter, der vor allem die Künste und die Freiheit des Denkens beflügelte. Das war auch das Jahrhundert der Entdeckungen. Kühne Seefahrer wagten sich über unbekannte Ozeane und benötigten dazu eine Möglichkeit zur Orientierung. Die Kugelgestalt der Erde war zwar seit dem Altertum bekannt, und das Koordinatensystem der Längen- und Breitengrade war ebenfalls eingeführt. Aber den eigenen Standort darauf zu verzeichnen, dazu benötigte man sowohl Navigationsverfahren als auch eine Karte. Beides war aus heutiger Sicht nur dürftig vorhanden. Gerhard Kremer, Kartograph und „Mathematikus“, der seinen Namen einer damaligen Sitte folgend zu Mercator latinisierte, hatte schon Globen und Atlanten für Mächtige und Kaufleute hergestellt, bis er die besonderen Anforderungen der Seefahrt erkannte und 1569 eine erste Weltkarte „ad usum navigantium“, soviel wie „zum Gebrauch in der Seefahrt“, herausgab und sie mit einer Beschreibung (Inspectori salutem) versah.
Daher kennen wir seine Gedankengänge. Sie besagen, dass man einen gleichbleibenden Kurs, d.h. gleichbleibender Schnittwinkel mit den Meridianen, auf einer gekrümmten Oberfläche nur dann als Gerade in einer ebenflächigen Karte darstellen kann, wenn man die Längengrade parallel macht, also mit wachsender Breite ost-westlich dehnt, und dass man gleichzeitig in gleichem Maßstab die Abstände der Breitenparallele vergrößern muss. Man nennt das „Winkeltreue“. Es sind also an jedem Ort zwei Verzerrungen nötig. Eine in Richtung der Längengrade, eine in Richtung der Breitengrade.
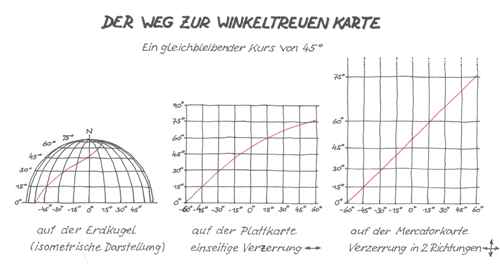Verzerrt man nur die Längengrade, bis sie parallel sind und behält die Abstände der Breitenparallele unverzerrt bei, so wie sie sich durch Abrollen der Erdkugel auf eine Ebene ergeben, also äquidistant, führt das zur „Plattkarte“. Die ist über begrenzte Entfernungen ebenfalls annähernd winkeltreu und wäre, z.B. für Revierkarten, durchaus zu gebrauchen. Für eine richtige Seekarte, zum Navigieren auf Meeren und Ozeanen mit der Präzision heutiger elektronischer Mittel, muss aber echte Winkeltreue durch exakt gleiche Verzerrung in Ost-West wie in Nord-Süd.–Richtung herbeigeführt werden.
Leider hat Mercator den erforderlichen Maßstab der Verzerrungen nicht mathematisch richtig erkannt. Er hat wohl erkannt, dass man das Problem nicht graphisch lösen kann (wie es die „Yacht“ suggeriert), sondern nur rechnerisch. Aber er hat mit Dreiecksanalogien und ihren Winkel- und Streckenbeziehungen gearbeitet und dabei Näherungen in Kauf nehmen müssen. Sie führten zu erstaunlich genauen Ergebnissen, wie seine im Originaldruck überlieferte Karte noch heute beweist. Aber sie befriedigten die Fachwelt zunächst nicht.
Nun kannte man schon seit Ptolemäus die trigonometrischen Winkelbeziehungen und hatte sogar schon gewisse Funktionstafeln. Mercator wusste also, dass mit wachsender geographischer Breite der Radius eines Breitenkreises sich mit dem Kosinus der Breite im Verhältnis zum Radius des Äquators verringert. Folglich sind die Meridiane auf jeder Breite mit dem Kehrwert des Kosinus dieser Breite auseinander zu zerren. Schwerer fiel es ihm, die Verzerrung der Breitenkreisabstände zu ermitteln. Denn diese wachsen „im Kleinsten“, also von Bruchteil zu Bruchteil eines Winkelgrades und summieren sich dabei auf. Das mathematische Werkzeug für diese Aufgabe wurde erst gute hundert Jahre später von Leibniz und Newton, und zwar gleichzeitig, gefunden. Es ist die Integralrechnung. Aber mit der Aufsummation endlich kleiner Winkeldifferenzen hätte man auch schon früher brauchbare Ergebnisse erzielt.
Nun wollen wir Mercator nicht vorhalten, was er hätte tun können. Die Nachfolgenden sind immer schlauer. Wahrscheinlich lag seine Stärke in der kartographischen Arbeit. Aber er hatte als erster den entscheidenden, richtigen Gedanken, wie Winkeltreue zu erzielen ist. Damit hat er seinen Namen zu Recht mit seiner Kartendarstellung verbunden. Häufig wird auch „Mercatorprojektion“ gesagt. Aber eine Projektion, also ein durch Strahlenwurf erzeugtes Abbild eines Objekts auf eine Fläche, ist es im eigentlichen Sinne nicht.
Mercators große Leistung war nicht die Schaffung der parallelen Meridiane auf seiner Karte. Die gab es auch schon auf anderen Kartendarstellungen. Es war die Erkenntnis, dass dazu die geeignete Streckung der Breitenkreisabstände gehörte, um eine echte Winkeltreue herzustellen. Heute nennen wir das „Vergrößerte Breite“. Sie lässt sich nur mit dem mathematischen Ausdruck ∫1/cos φ*dφ errechnen, nicht jedoch anschaulich graphisch mit Zirkel und Lineal ermitteln. Wenn man so will, war er Leibniz und Newton um 100 Jahre voraus, besser gesagt, er hat das Problem definiert, für das diese beiden dann die Lösung gefunden haben.